Math'φsics

Menu
  • Acceuil
  • Maths
  • Physique
    • Maths
    • Physique
  • Théorème de Kakutani

    Formulaire de report

    START
    Théorème
    Théorème de Kakutani Hypothèses:
    • \(X_1,X_2,\dots\) est une sutie de Variables aléatoires indépendantes
    • elles sont à valeur dans \(]0,+\infty[\) et d'espérance \(1\)
    • \(M_n:=X_1\times\dots\times X_n\) \(\to\) c'est une Martingale positive, donc elle converge \(\overset{ps}\,\) vers \(M_\infty\geqslant0\)

    Résultats:
    • on a l'équivalence :
            
      1. \({\Bbb P}(M_\infty\gt 0)=1\)

        
  • \({\Bbb E}[M_\infty]=1\)
    •     
  • \((M_n)_{n\geqslant0}\) est uniformément intégrable
    •     
  • Si \(a_n:={\Bbb E}[\sqrt{X_n}]\), alors $$\prod^{+\infty}_{n=1}a_n\gt 0$$
    • si ces propriétés ne sont pas satisfaites, alors \({\Bbb P}(M_\infty=0)=1\)

    Equivalence?:
    Résumé: Permet de caractériser les cas où un produit de v.a. D'espérance \(1\) a une limite strictement positive.
    END
    Démontrer \((ii)\implies(i)\) :

    Puisque l'espérance est \(1\gt 0\), la probabilité d'être \(\gt 0\) est \(\gt 0\).

    On conclut via la Loi du tout ou rien de Kolmogorov.


    Démontrer \((iii)\implies(ii)\) :

    Les martingales u.i. Convergent dans \(L^1\) (et \(\overset{ps}\,\)).

    On peut donc passer l'espérance à la limite.


    Démontrer \((iv)\implies(iii)\) :

    On pose \(N_n\) le produit des \(\frac{\sqrt X_k}{a_k}\) pour \(k\leqslant n\).

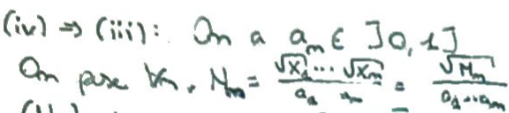
    C'est une martingale positive, donc elle converge \(\overset{ps}\,\).

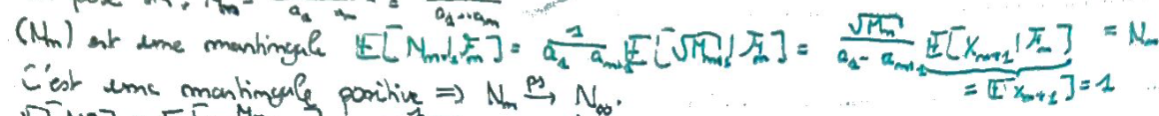
    On peut montrer que cette martingale est bornée dans \(L^2\).

    On utilise l'Inégalité de Doob dans Lp pour obtenir une domination \(L^1\) de \((M_n)_n\).

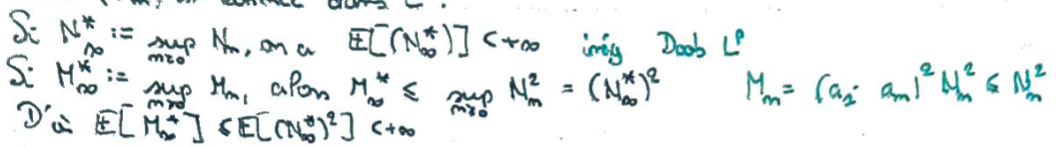
    Cette domination \(L^1\) nous donne l'uniforme intégrabilité.


    Démontrer \((i)\implies(iv)\) :

    On va procéder par l'absurde.

    On pose \(N_n\) le produit des \(\frac{\sqrt X_k}{a_k}\) pour \(k\leqslant n\).

    Alors \(M_n\overset{ps}{\underset{n\to+\infty}\longrightarrow}0\), ce qui est absurde par \((i)\).